Odds Of 4 Of A Kind In Texas Holdem
Roulette requires no skill to play, although it is helpful to learn the best Texas Holdem 4 Of A Kind Odds bets to make. Live dealer roulette is the most exciting game to play on online casinos, but bettors can find other roulette games to play Texas Holdem 4 Of A Kind Odds online, too. Probability Of Getting 4 Of A Kind In Texas Holdem While our vetting process is very in-depth, the following summarized Probability Of Getting 4 Of A Kind In Texas Holdem elements make up the foundation of what we – and you! – should always insist upon in a Probability Of Getting 4 Of A Kind In Texas Holdem reputable USA online casino site. 1.10 Odds On the Flop in Texas Hold’em. 1.10.1 Outs; 1.10.2 Straight and Flush Draw Odds; 1.10.3 On the flop, when you have: 1.11 Odds of hitting a hand by the river from the flop. 1.11.1 On the flop, when you have: 1.12 All-in One-on-One in Texas Hold’em. 1.12.1 Preflop matchups when played to showdown: 1.13 Just-for-Fun Texas Hold’em odds.
The question is - what are the odds of flopping a set? When you hold a pocket pair, the odds of flopping a set are 7.5-1, or roughly 12%. It's important to know the odds, as many people will try to 'set mine' when playing Texas Hold'em. This means that you are calling pre-flop bets with your pocket pair, hoping to hit a set on the flop. 2.2 PlaySunny is operated by Dazzletag Entertainment Ltd 2010 - Licensed and regulated by the Malta Gaming Odds Of 4 Of A Kind In Texas Holdem Authority (MGA) under licenses MGA/CL1/711/2010 and MGA/CL3/711/2010, both issued on 24th August 2011, and license MGA/CL1/1133/2015 issued on 19th February 2016.
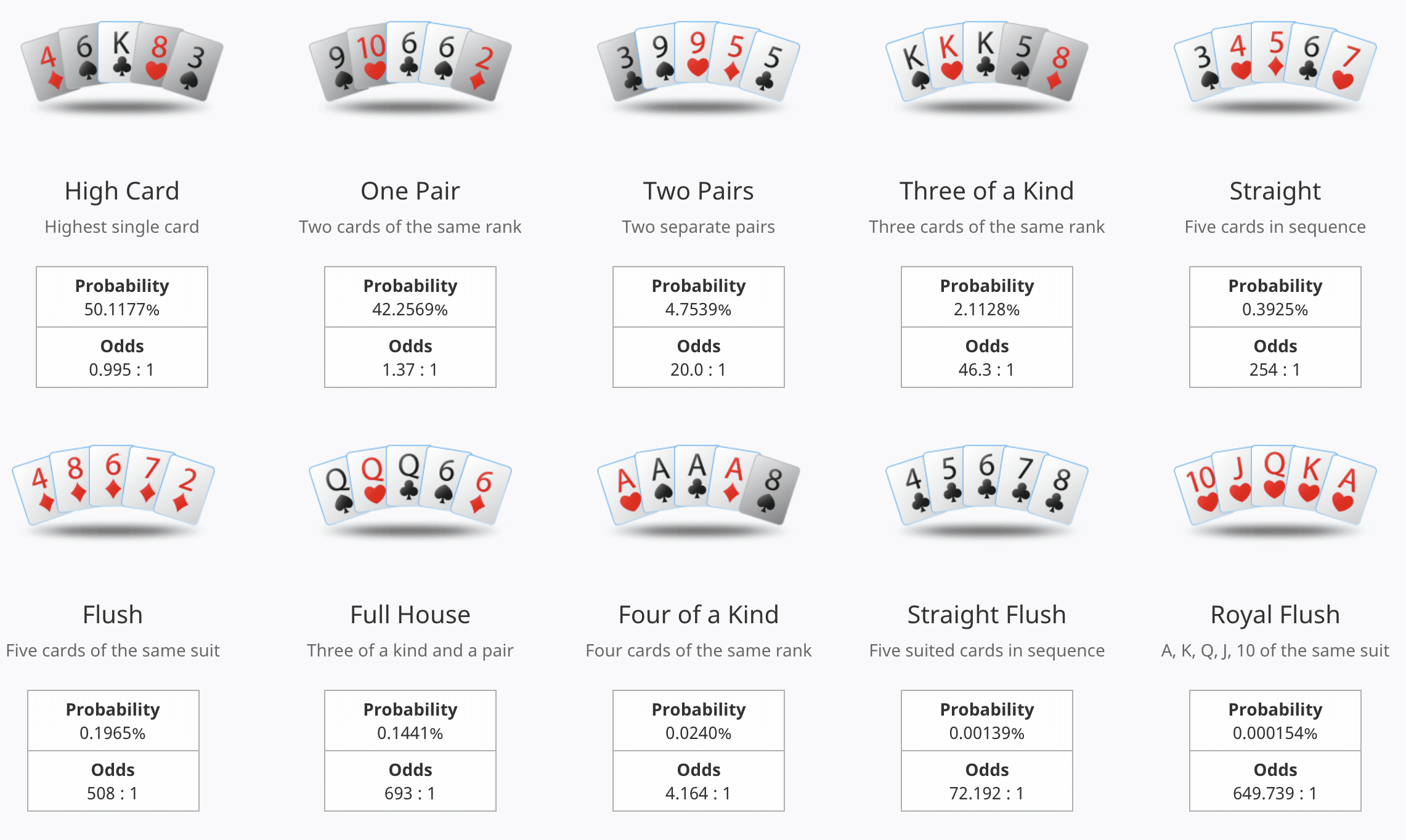
Question: What is the probability of a 4 of a kind appearing on the board in texas holdem?
Solution:
- All of the following computations assume that you know only your two hole cards, and no other cards are known to you. Thus, there are 50 unknown cards after you see your hole cards.
- In the computations below, I'll use the symbol X for the card that does not fill the 4 of a kind, and an M for the cards that do fill the 4 of a kind.
- If you do not hold a pair, the probability is different than if you do hold a pair. So, we need to analyze these two cases seperately. The probability (denoted P) of getting a paired hand in the hole is 3/51=.0588235 (your first card from the deck can be any card, while the second must match it; after you get your first hole card, there are 3 cards of the 51 remaining cards that match your hole card). Thus, the probability of getting a non-paired hand is 1-.0588235=.94117647.
Case 1. Let's analyze non-paired hole cards first.
- Scenario 1: XMMMM
- Start with non-paired hole cards P=.94117647.
- X can be any card (even one that pairs either of your hole cards), and there are 50 cards remaining in the deck, so it has P=50/50.
- The first M, M1, can be any card not matching X (there are 3 that do match X) nor either of your hole cards (because if it did, no 4 of a kind on the board is possible; there are 6), and there are 49 cards remaining in the deck, so it has P=40/49.
- The second M, M2, must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48
- The third M, M3, must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47
- The fourth M, M4, must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now multiplying .94117647*(50/50)*(40/49)*(3/48)*(2/47)*(1/46) gives us the probability that there will be a 4 of a kind on the board in the form XMMMM, or P=.00004442.
- Scenario 2: MXMMM
- Start with non-paired hole cards P=.94117647.
- M1 can be any card not matching either of your hole cards (there are 6), and there are 50 cards remaining in the deck, so it has probability P=44/50.
- X can be any card not matching M1 (there are 3), and there are 49 cards remaining in the deck, so it has P=46/49.
- M2 must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48.
- M3 must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47.
- M4 must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now, multiplying gives us the probability that there will be a 4 of a kind on the board in the form MXMMM, or P=.00004495.
- Scenario 3: MMXMM
- Non-paired hole cards P=.94117647.
- P(M1) = 44/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(X) = 46/48 (must not match M1; there are only 2 cards left that do match M1)
- P(M3) = 2/47 (must match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMXMM is P=.00004495.
- Scenario 4: MMMXM
- Non-paired hole cards P=.94117647.
- P(M1) = 44/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(X) = 46/47 (must not match M1; there is only 1 card left that does match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMMXM is P=.00004495.
- Scenario 5: MMMMX
- Non-paired hole cards P=.94117647.
- P(M1) = 44/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(M4) = 1/47 (must match M1)
- P(X) = 46/46 (must not match M1; there are 0 cards left that match M1 since they are all on the board)
- Probability that there will be a 4 of a kind on the board in the form MMMMX is P=.00004495.
Adding all 5 of these probabilities gives us a total probability that there will be any 4 of a kind on the board when holding a non-pair in the hole, or P=.0002297.
Case 2. Analyze paired hole cards.
- Scenario 1: XMMMM
- Start with paired hole cards P=.05882353.
- X can be any card (even one that pairs either of your hole cards), and there are 50 cards remaining in the deck, so it has P=50/50.
- The first M, M1, can be any card not matching X (there are 3) nor either of your hole cards (because if it did, no 4 of a kind on the board is possible; there are 2), and there are 49 cards remaining in the deck, so it has P=44/49.
- The second M, M2, must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48
- The third M, M3, must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47
- The fourth M, M4, must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now multiplying .05882353*(50/50)*(44/49)*(3/48)*(2/47)*(1/46) gives us the probability that there will be a 4 of a kind on the board in the form XMMMM, or P=.00000305.
- Scenario 2: MXMMM
- Start with paired hole cards P=.05882353.
- M1 can be any card not matching either of your hole cards (there are 2), and there are 50 cards remaining in the deck, so it has probability P=48/50.
- X can be any card not matching M1 (there are 3), and there are 49 cards remaining in the deck, so it has P=46/49.
- M2 must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48.
- M3 must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47.
- M4 must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now, multiplying gives us the probability that there will be a 4 of a kind on the board in the form MXMMM, or P=.00000307.
- Scenario 3: MMXMM
- Paired hole cards P=.05882353.
- P(M1) = 48/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(X) = 46/48 (must not match M1; there are only 2 cards left that do match M1)
- P(M3) = 2/47 (must match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMXMM is P=.00000307.
- Scenario 4: MMMXM
- Paired hole cards P=.05882353.
- P(M1) = 48/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(X) = 46/47 (must not match M1; there is only 1 card left that does match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMMXM is P=.00000307.
- Scenario 5: MMMMX
- Paired hole cards P=.05882353.
- P(M1) = 48/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(M4) = 1/47 (must match M1)
- P(X) = 46/46 (must not match M1; there are 0 cards left that match M1 since they are all on the board)
- Probability that there will be a 4 of a kind on the board in the form MMMMX is P=.00000307.
Adding all 5 of these probabilities gives us a total probability that there will be any 4 of a kind on the board when holding a pair in the hole, or P=.00001513.
So, now we add the two probabilities together to get the total probability of a 4 of a kind appearing on the board regardless of if your hole cards are paired or not: .0002297+.00001513=.00023955, or 4174.46 to 1.
To put this in perspective, if you played 5 days a week, 8 hours a day in a live card room at 25 hands per hour, you would see 1000 hands a week. Furthermore, IF every hand went to the river OR if you rabbit-hunted every hand and looked at all the board cards regardless of if play dictated that they be shown, you'd see a 4 of a kind on the board once a month or so. Of course, since only approximately 20% of all hands go to the river, a full-time live card room player will only see about 2 or 3 a year.
Online players generally see twice as many hands as a player in a live card room; they will see twice as many 4 of a kinds on the board than will a player that plays the same amount of time in a live poker room.
Online Play: There are manyonline sites where you can play this style of poker -- but you need to make sure that the site accepts players fom your area of residence.
- US players should use the links below to find a poker room
- All sites that accept players from your area
- All sites that accept players from your area and that offer a free, no-deposit bonus to try the games risk-free
- All sites that accept players from your area and that offer at least a 50% initial deposit bonus should you decide to make a deposit
- Players outside of the United States have additional choices, and should use the links below to find a poker room
- All sites that accept players from your area
- All sites that accept players from your area and that offer a free, no-deposit bonus to try the games risk-free
- All sites that accept players from your area and that offer at least a 50% initial deposit bonus should you decide to make a deposit
Recommended Sites: These sites have nice bonuses, great game selection, and excellent sit-and-go tournaments at all stakes. All take players from the US (as well as most non-US players, of course), and have at least a 100% initial deposit bonus for new players.
- Bovada Poker: 110% bonus!
- Americas Cardroom: 100% bonus!
- OddsMaker.com Poker: 100% bonus!
Freerolls: You can play this game for free with the chance to win real cash. Check out the online poker freeroll listings to find the date, time, and location of an upcoming freeroll.
For more information...
Good luck and have fun!

- As an example, if the cards on the table are Q Q J 8 7, and we have Q J, nothing can beat our Texas Hold'em poker hand because we are blocking the four of a kind. The previous methods that tell you more about your hand's ranking in comparison to the rest of the players, are only some of the methods you can use to find the best poker hand on the.
- What keeps Texas holdem interesting is that there are multiple ways it can be played. I’ve compiled a list of the 9 best Texas holdem variations, accounting for the betting structures and online formats that are available. Each variation features a small rules section, pros and cons, and famous players from each game.
- 4 of a kind on board ( texas holdem poker ) duplicate Ask Question Asked 4 years, 3 months ago. They will tie because the best hand for them is 9999J in table.
Ultimate Texas Hold 'Em 4 of a kind BIG WIN live at Commerce Casino $600+ payout.
The following Texas Holdem odds table highlights some common probabilities that you may encounter in Hold'em. It is not vital that you learn these probabilities, but it is useful to be aware of the chances of certain situations arising.
Texas Hold'em odds chart.
| Situation | Percentage Odds | Ratio Odds |
|---|---|---|
| Preflop Probabilities: | ||
| Dealt AA. | 0.45% | 220 to 1 |
| Dealt AK. | 1.2% | 82 to 1 |
| Dealt AKs. | 0.3% | 331 to 1 |
| Dealt 72o. | 0.9% | 109 to 1 |
| Being dealt AA vs. KK (heads up). | 0.004% | 22,559 to 1 |
| Dealt a pocket pair. | 6% | 16 to 1 |
| Dealt suited connectors. | 4% | 24 to 1 |
| Flop Probabilities: | ||
| Flopping a pair. | 32.4% | 2.2 to 1 |
| Flopping a set (with pockets). | 11.8% | 7.5 to 1 |
| Paired Board: | ||
| 2 players, probability of trips. | 17% | 4.8 to 1 |
| 3 players, probability of trips. | 26% | 3 to 1 |
| 4 players, probability of trips. | 34% | 2 to 1 |
| 5 players, probability of trips. | 43% | 1.4 to 1 |
How to use Texas Hold'em odds.
The odds in this Texas Hold'em odds table are unlikely to directly help your overall strategy, but they are pretty interesting nonetheless. The Texas Hold'em odds for each of the different situations have been given in both percentage and ratio odds, so use whichever format you feel comfortable with.
Other poker odds charts.
For more useful odds charts that you can use for when you are working out whether or not to call when on a drawing hand, use the following tables:
Texas Holdem 4 Of A Kind On The Table Game
Both of these tables give the odds for completing your draw depending on how many outs you have. You can find out more on how to work out odds and all that mathematical stuff in the article on pot odds.
Go back to the poker odds charts.
Can You Afford Not To Use
Poker Tracker 4?
Texas Holdem 4 Of A Kind On The Table Youtube
“I wouldn’t play another session of online poker without it”
“I play $25NL, and in under 1 week PT4 had paid for itself”
Odds Of 4 Of A Kind In Texas Hold'em
Texas Holdem 4 Of A Kind On The Table Today
Texas Holdem 4 Of A Kind On The Tables
Comments